Game Introduction

Pokémon GO may be the most popular mobile game in the world in 2016. It uses the technology of augmented reality to attract players to catch virtual creatures on the street. The players use the camera of a mobile phone to interact with the environment as if they were catching real creatures in the world.

There are also gyms, where Pokémon trainers (players) can deploy their Pokémon caught. The trainers all over the world are divided into three teams, with each team having the goal of seizing gyms of other teams as well as defending their own.

Of course, trainers want to catch and use the most powerful Pokémon. Here comes the question: Which Pokémon is the most powerful? To answer this question, we need one or several measures. The game itself provides a measure called CP. However, after mining the application, players found that Pokémon have latent stats and that CP does not reflect the battle ability very well.

This post starts with proposing several measures as evaluation of Pokémon’s battle capacity. The measures vary according to the scenario as well as the objective of the trainer. Then, this post designs methods to evaluate the meta, which is the whole battle ecosystem of the game. Lastly, it gives the way to choose an attack team for any given gym. This post is written for hard-core players who have studied the game and want to improve their playing efficiency.

This research was accomplished during the Christmas of 2016. Therefore, the data it used are all outdated now since Niantic (the company behind Pokémon GO) periodically modifies the data. However, even though the data may be altered, the battle mechanic stays the same. The measures and methods proposed in this post can be directly applied to the new data. I believe that this research is still relevant.

Evaluation of Pokémon

This section has a lot of overlap with the research of Gamepress. Chronically, I did this research much earlier but have not had the luxury to publish it. Then, the researchers of Gamepress independently developed similar approaches later.

Let us denote species as the set of Pokémon sharing the same NO. in Pokédex. According to Reddit users’ mining, besides HP and CP and other explicit measures, each species has 3 latent stats: attack, defense, and stamina. When the Pokémon level up, these species specific stats will not change. Instead, its level serves as a multiplier applied on these latent stats.

Indeed, the damage formula indicates that the damage is proportional to the attacking monster’s attack stat and inversely proportional to the defending monster’s defense stat. Based on this discovery, we can define

• power of the 1st kind: [ \text{attack} ]
• power of the 2nd kind: [ \text{attack} \times \text{defense} ]
• power of the 3rd kind: [ \text{attack} \times \text{defense} \times \text{stamina} ]

Here, I avoided the term “type” by using the word “kind” so as not to be confused with a Pokémon’s type.

These formulae are embarrassingly simple but have realistic interpretation. Species having the highest power of the 1st kind deals the most damage per time unit. It is best when facing opponents with a lot of HP, or when your battery is running low, or when you do not have much time. Species having the highest power of the 2nd kind deals the most damage per HP loss. It is best when you are running out of potions, especially for rural trainers, who do not encounter PokéStops so often. Species having the highest power of the 3rd kind deals the most damage per monster slot. You can only use a team of 6 Pokémon in total for each gym match. However, the most prestigious gym may have 10 Pokémon, which makes the monster slots precious.

On the other hand, the in-game measure CP’s formula is proportional to [ \text{attack} \times \sqrt{\text{defense} \times \text{stamina}} ] Obviously, it underestimates the power of the 3rd kind, which is regarded as the overall power of a species. This observation has important consequences. When one levels up a Pokémon, its CP grows linearly (i.e., a fixed amount per level up) until Level 30 because the level multiplier aforementioned is roughly a square root function of the level before Level 30. With that in mind, the power of the 3rd kind will be proportional to $\text{level}^\frac{3}{2}$, which is a super-linear function. The super-linearity implies that the more you level up your Pokémon (before Level 30), the more power increment of the 3rd kind you gain. Of course, since you need more resource to level up in higher levels than in lower levels, one cannot simply draw the conclusion that it is more beneficial per resource in higher levels.

The following table shows the power of the 2nd and the 3rd kind of the top species before and after the first stats adjustment taking place in November 2016. The numbers show the relative power of each species. Species names in gray have dropped from the top 10, while species names in bold are new members of the top 10.

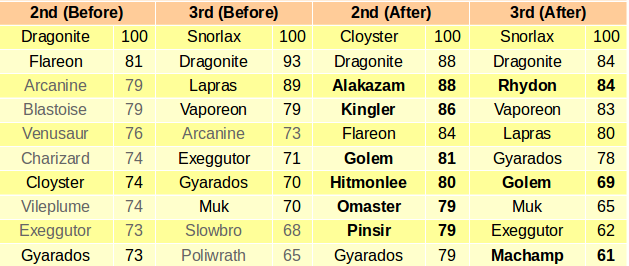
As a side note, one can also develop similar measures for gym training, also known as battling with a friend gym to increase its prestige. Dividing the above three measures by CP, we can roughly get some idea of which species is the most efficient in earning prestige in terms of time, potion and slot respectively.

The above three measures are just the first step towards the evaluation of species, for it does not consider the moves owned by the species. Some species have more powerful moves than others, and we should take that into account. Each Pokémon has a quick move and a charge move. Quick moves are less powerful, but they do not need any energy, usually take less time to cast, and help in generating energy. Charge moves are powerful, but they consume energy and usually take quite a while to cast. What we feel like measuring is the DPS (damage per second) – one can, of course, use a different time unit other than second without the risk of breaking the idea. It is not difficult to calculate the DPS for either quick moves or charge moves, but what we want is the overall DPS of the combination of the two.

I propose the following formula [ \frac{\text{QP} \times \text{Stab} + \frac{\text{EG}}{\text{EC}} \times \text{CP} \times \text{Stab}}{\text{QD} + \frac{\text{EG}}{\text{EC}} \times \text{CD}}]

• $ \text{QP} $: quick move power
• $ \text{CP} $: charge move power
• $ \text{QD} $: quick move duration
• $ \text{CD} $: charge move duration
• $ \text{EG} $: quick move energy generation
• $ \text{EC} $: charge move energy consumption
• $ \text{Stab} $: quick or charge move Stab

It is a duration weighted average of the power of the quick move and the charge move. To get the formula for defensive Pokémon, add 2 (seconds) to both $ \text{QD} $ and $ \text{CD} $. If you suppose that the opponent will dodge the charge move, divide $ \text{CP} $ by 4. If the charge move’s DPS is lower than the quick move’s, take directly the quick move’s DPS.

This is an approximate estimation of the true overall DPS, for it ignores some minor details in the battle mechanic. For example, each HP loss will generate 0.5 energy, which makes the above estimation underestimate the true DPS. A Charge move can overkill, which makes the estimation overestimate the true DPS. I believe that, overall, it is a good estimate.

By multiplying the power of the species with the DPS of the move combination, we get a score for each Pokémon. The following table shows the scores of the 2nd and of the 3rd kind of the top species before and after the first stats adjustment taking place in November 2016. Each species uses the move combination dealing the highest DPS. The numbers show the relative score of each species. Species names in gray have dropped from the top 10, while species names in bold are new members of the top 10.

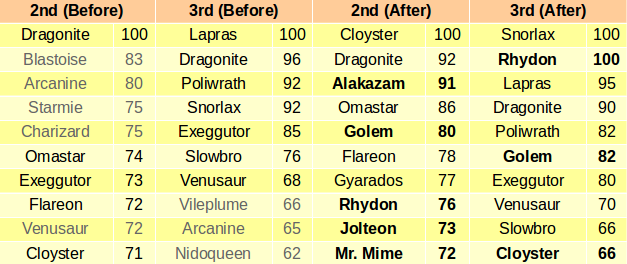
This table concludes this section, where we learn the most powerful Pokémon.

Relative strength

The previous section adopts a static point of view of the game, without considering the type efficiency in Pokémon GO. For example, water type Pokémon are efficient against fire type Pokémon. Therefore, a strong Pokémon can be less relevant if there exists a strong counter. This encourages us to use pairwise scores to measure the relative strength of each pair of Pokémon.

Luckily, we can reuse the formulae in the previous section. For each pair of Pokémon, we multiply the type efficiency along with $\text{Stab}$ in the DPS formula. Then, we divide the attacking Pokémon’s score (of any kind) by twice the defending Pokémon’s score of the 3rd kind. We call this quotient relative score. Thus, all relative scores form a payoff matrix.

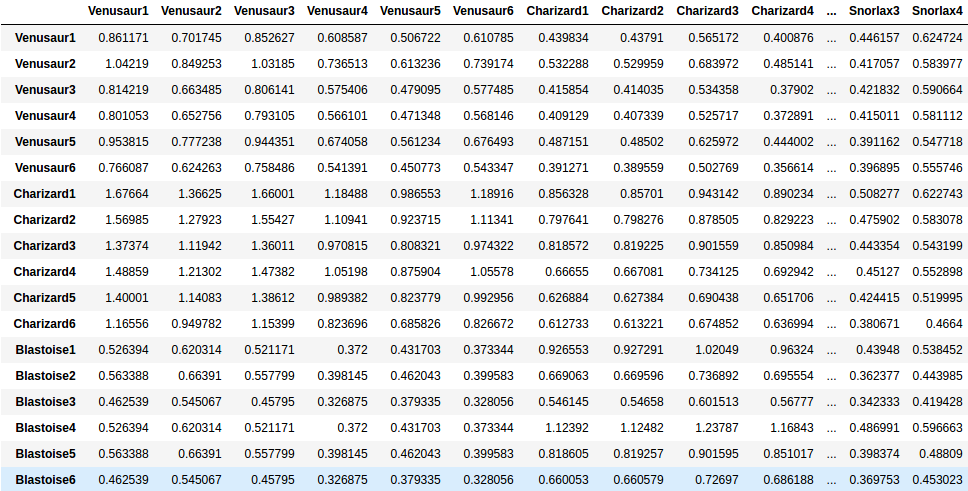
You can also use battle simulation as the researchers in Gamepress do to form the relative scores. It unavoidably will need a loop for each battle, which may be computationally prohibitive when the number of species gets large. Besides, you have always to make decisions during the battle simulation and the best choice is not evident. For now, I will just stick to my straightforward relative score and believe that it is an accurate estimator of the reality.

Denote $A$ as the payoff matrix, whose rows correspond to attacking Pokémon and columns defending Pokémon. We can define a Pokémon $j$’s defense power as the highest relative score when attacked by any Pokémon. Mathematically, [ V(j) := \max_i A(i,j) . ] Then, the best defender will be the Pokémon yielding the lowest relative score. Mathematically, [ j^\star := \arg\min_j V(j) ] Then, the best attacker will be the Pokémon yielding the highest relative score against the best defender. Mathematically, [ i^\star := \max_i A(i, j^\star) ] Applying these definitions on the old and new data (using the power of 3rd kind), Lapras and Arcanine are the best defender and the best attacker respectively before the stats adjustment; Snorlax and Ryhdon are the best defender and the best attacker respectively after the adjustment.

The above deduction uses the so-called minimax criterion, which considers the worst case: a defender will always encounter its best counter. In reality, this is not always the case: Some Pokémon may be rarer than others, and not every trainer can get every Pokémon. The minimax criterion is therefore rather pessimist for defending Pokémon. For example, Arcanine had long been rare, which made Lapras an even tougher defender.

Another problem concerning the minimax criterion is that it supposes everyone can have the strongest defender, which is not true. In fact, Lapras had been (and always is) even rarer than Arcanine. Gyms were thus mostly inhabited by water type Pokémon such as Vaporeon for its extremely high CP and easy accessibility. In that case, a grass type Pokémon such as Venusaur and Exeggutor may be more valuable as attacker.

To take the popularity of the Pokémon into consideration, we can adopt the Bayesian approach. Since I do not have any data about the popularity, I have to restrain myself from doing this research. Instead, let us suppose that each species is equally popular and do some other research but still stick to the payoff matrix.

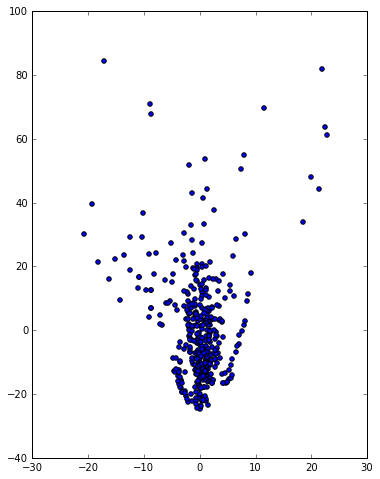
Let us consider each row of the payoff matrix (3rd kind) as a point in some high-dimensional space, execute a principal component analysis, and project the points onto the plane generated by the 1st and 2nd component as well as onto the one generated by the 2nd and 3rd component. The following figures use the data before the adjustment, where we observe that the left figure is quite like a pyramid and that the right figure is a vertical view of this pyramid.

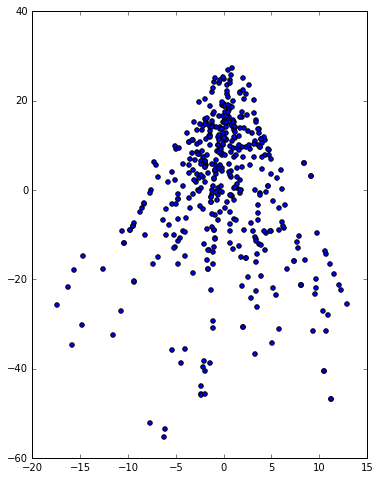
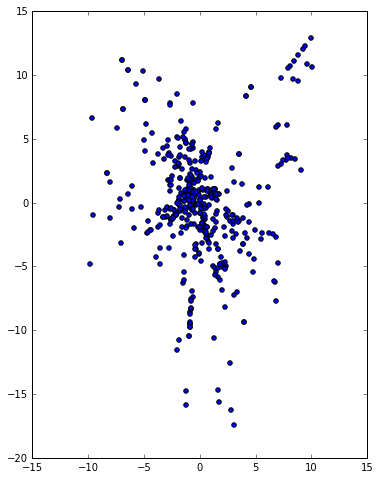
Now let us see what Pokémon these points stand for. In the left figure, all strongest Pokémon sit at the bottom, with Dragonite the lowest, while the apex contains the weakest Pokémon. In the right figure, we observe that the strongest Pokémon are clustered. The downside is fire type Pokémon, the upper right corner is grass type Pokémon, and the upper left corner is water type monster. Snorlax, a normal type monster, sits in the middle. Slightly above Snorlax lie Slowbro, Gyarados and Nidoqueen, which slightly counter fire type Pokémon and are weak to grass type Pokémon.

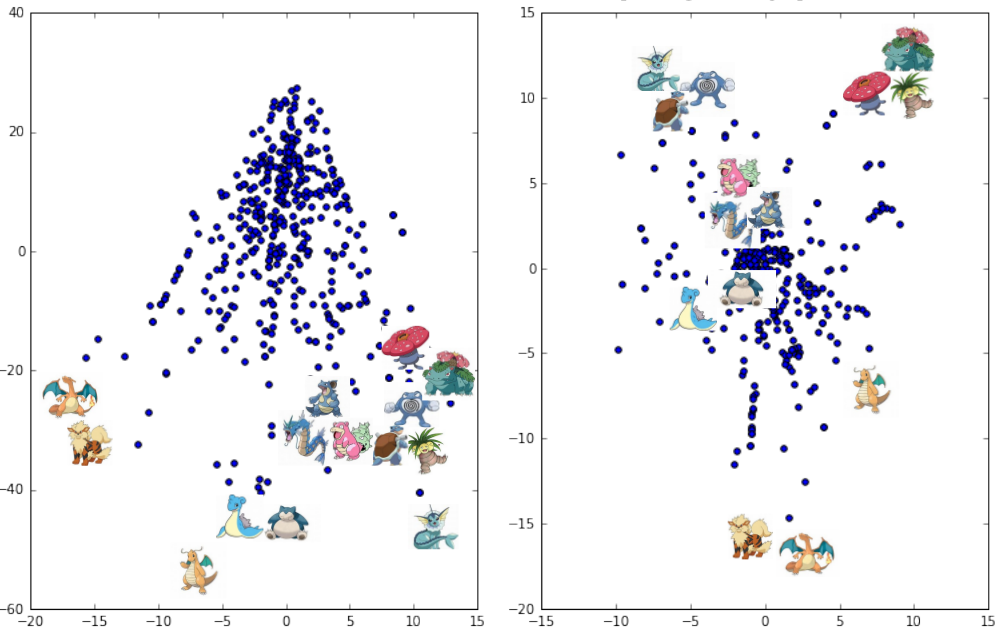
To sum up, there are 3 axes, with each axis correspondent to a type among fire, grass, and water. If you calculate the payoff matrix of Rock-paper-scissor and do the same principal component analysis, you will find exactly the same pattern. In other words, Pokémon GO is essentially a Rock-paper-scissor.

Now let us use the data after the adjustment. From the left figure below, we see the (relative) buff and nerf of this adjustment: Arcanine and Dragonite are nerfed; Vaporeon is buffed; Rhydon and Golem suddenly appear as powerful monsters; Grass and water type Pokémon mostly disappear. From the right figure, we observe a 4th axis at the upper left corner: the rise of the rock and ground type, which replaces water type as the best counter against the fire type. Therefore, the new 3 axes are fire, grass, and rock/ground. Water is still relevant because of Vaporeon, which forms a sub-axis.

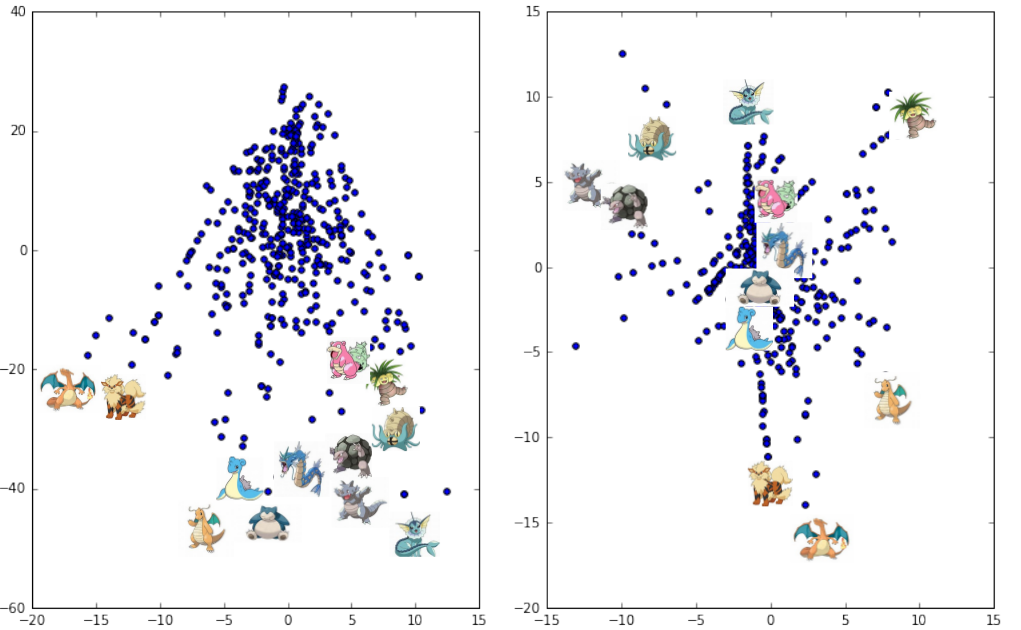
After studying the attacking Pokémon, we consider now the defending Pokémon. By considering each column of the payoff matrix as a point and doing the same analysis as above, we get the following figures. The left figure is like an upside-down pyramid, and the right one is the vertical view. Interestingly, this time the strongest Pokémon still sit at the bottom. That is, they are at the apex! In other words, they are at the middle in the right figure. This implies that the strongest defenders are those type neutral ones. They have either normal type or their moves complement their type weakness.

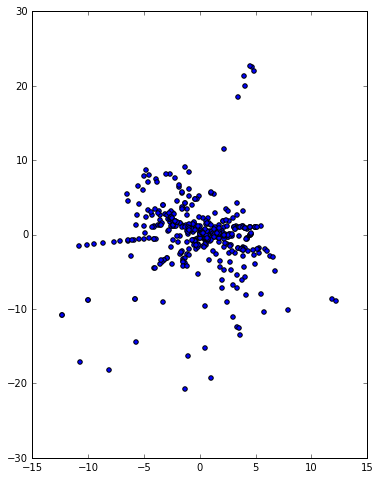
For those interested in the name of these strongest defenders, they are Lapras, Dragonite, Snorlax, Poliwrath, Exeggutor, and Slowbro before the adjustment, with Rhydon and Golem in addition after the adjustment.

Gym battle team choice

With the guide of the previous section, maybe you all own the strongest attackers and defenders now. Then, a new problem comes: Which 6 Pokémon should I choose to battle a gym? For each defender, of course, I have the best attacker, but what if there are more than 6 defenders in the gym? How should I balance my team? This section will answer this question.

For a given gym and a given inventory, we can calculate a payoff matrix of 3rd kind $(a_{ij})$. $(x_{ij})$ is a matrix of the same size. $x_{ij}$ equals 0 if we shall not use Pokémon $i$ (in your inventory) to battle Pokémon $j$ in the gym and equals 1 if we shall use Pokémon $i$ to battle Pokémon $j$ until $i$’s faint. If it equals some value in $(0,1)$, then we say that we use $i$ to battle $j$ until $x_{ij}$ portion of $i$’s HP is gone. Let $c_i$ denote the HP of Pokémon $i$. I propose to solve the following optimization problem:

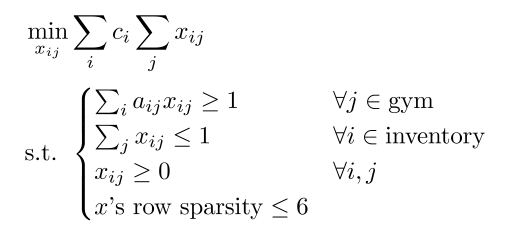
The first constraint means that every Pokémon in the gym is going to be beaten. The second constraint means that you will not overuse your Pokémon (e.g., use a fainted Pokémon to battle). The third constraint means that you will not gain HP during the battle. The fourth constraint means that you can at most use 6 Pokémon. Any $(x_{ij})$ satisfying these 4 constraints is a qualified team candidate able to beat the gym. You may want the qualified team that has the least HP loss, and hence the objective function.

This optimization problem is almost a linear programming problem (which is known to be easy to solve) except for the 4th constraint. Therefore, I introduce a few 0/1 auxiliary variables $(z_i)$ and propose to solve the following optimization problem, which is equivalent to the previous one. This is a zero-one linear programming and should not be too difficult.

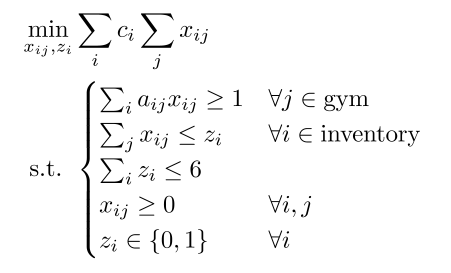
We see that all these equations are linear with regard to $x_{ij}$. There are no cross items such as $x_{ij}x_{kl}$, which means there is no interaction between Pokémon in your team. Every Pokémon battles for its own purpose.

This simplicity is different from the original game, where you can assign different roles to each Pokémon in your team: Some Pokémon set the scenario, others sweep out the opponent’s Pokémon…

In Pokémon GO, there are still some strategies. For instance, you can use a near-faint Pokémon to “eat” the charge move so as to protect your other Pokémon. However, the strategies are, overall, very limited.

Is the lack of strategies a problem? Not that much. Pokémon GO is an AR game, which encourages people to get out. It is possible to attract hard-core players by letting them spend days at home in thinking about the strategies, but it is unnecessary for the success of an AR game. On the contrary, I would like to see some large-scale strategies such as the ones in Ingress, as opposed to the battle strategies in the original games.

Summary

For those who skip the content and get directly here, I will highlight the main results. You can use each of 3 measures proposed in this post as opposed to the CP to evaluate Pokémon’s battle capacity, with each measure for a different purpose. A formula of the overall DPS is explicitly given. Payoff matrices are used to quantify the relative power of each pair of Pokémon (attacker and defender). Strong attackers are strong in different aspects, while strong defenders are all “alike”. Since there is no interaction between Pokémon in your team, you can use zero-one linear programming to choose your gym battle team. Pokémon GO is a relatively easy game compared with the original game. Pokémon GO is almost a rock-paper-scissor.

You may also like

• Using the Nash Equilibrium to build a minimalist PvE list for Pokémon GO