Using the Nash Equilibrium to build a minimalist PvE list for Pokémon GO
Abstract. This post introduces the concept of Nash Equilibrium into Pokémon GO meta-game, with the intention to build a minimalist PvE list. The idea is to build an all-round team for gym battles or for boss raids with few Pokémon. This approach allows the players to concentrate their resources to build a small team of strong Pokémon instead of a large group of mildly strong Pokémon. To demonstrate the usage of the Nash Equilibrium, I use Timeout as the win condition for gym battles and total damage output for boss raids. The resulting minimalist lists are for reference; I provided, at the end of the post, the dataset and the code necessary for the readers to build their own minimalist lists.
Introduction
Recently the GamePress user Grand_Champ posted a solution to counter all 18 types with just 4 Pokémon. This minimalism is appreciated since, in Pokémon GO, the resources are scarce and you want to concentrate them on only a few Pokémon.
However, as some other users (e.g., Ziperro, Ransen) pointed out, Grand_Champ’s approach has the following flaws:
- Some Pokémon have dual types, which cancels some weaknesses.
- Defender Pokémon may have moves that counter your counter.
- It fails to address the factor how the gym defending strategy will evolve given this minimalist attacking team.
For this sake, I propose to use the Nash Equilibrium to address this question. It has the following advantages:
- It factors in all battle information, not only the type information.
- It also gives a defender Pokémon list.
- When both the attacker team and the defender team use the list given by the Nash Equilibrium, neither of them can do better with a unilateral change. That is, any effort to deviate from the equilibrium will be punished.
The third point implies that you can safely invest your resources on these Pokémon without worrying about the other player’s strategy.
In the following, I will use an example to explain the Nash equilibrium and then present the methodology and the calculation results. At the end of the post, I will also link to the code I wrote to conduct this computation.
Nash equilibrium
Supposing Player A and Player B are playing a multi-round Rock-paper-scissors. They have to decide a static strategy at the start of the game.
If Player A’s strategy is to always choose Rock, the worst case for him will be that Player B always chooses Paper. Is there any way to mitigate the worst case loss?
The answer is to use a hybrid strategy: pick Rock, Paper, or Scissors with equal probability. Then, regardless of Player B’s strategy, Player A’s worst-case loss is 0 on average. If Player B thinks like Player A, then they will both adopt this strategy.
If one deviates from this strategy, then the other player can modify his strategy accordingly to take advantage. Therefore, neither of them will deviate from that strategy, both of them will stick to it. This idea is essentially the Nash Equilibrium.
Data
- The data I used was last updated on October 15, 2018, provided by Reddit user UW_Unknown_Warrior. I believe that it is the up-to-date version and precisely reflects the current (Mars 2019) environment.
- The type effectiveness bonus is set to 1.6 (instead of 1.4).
- The STAB bonus is set to 1.2.
- No legacy moves.
Payoff matrix
The payoff matrix is the key to compute the Nash equilibrium. In the payoff matrix,
- each row represents an attacker,
- each column represents a defender,
- each cell represents the relative strength between the attacker and the defender.
The following is the visualization of such a payoff matrix.
The green color means that the attacker has an advantage, while the violet color means that the defender has an advantage.
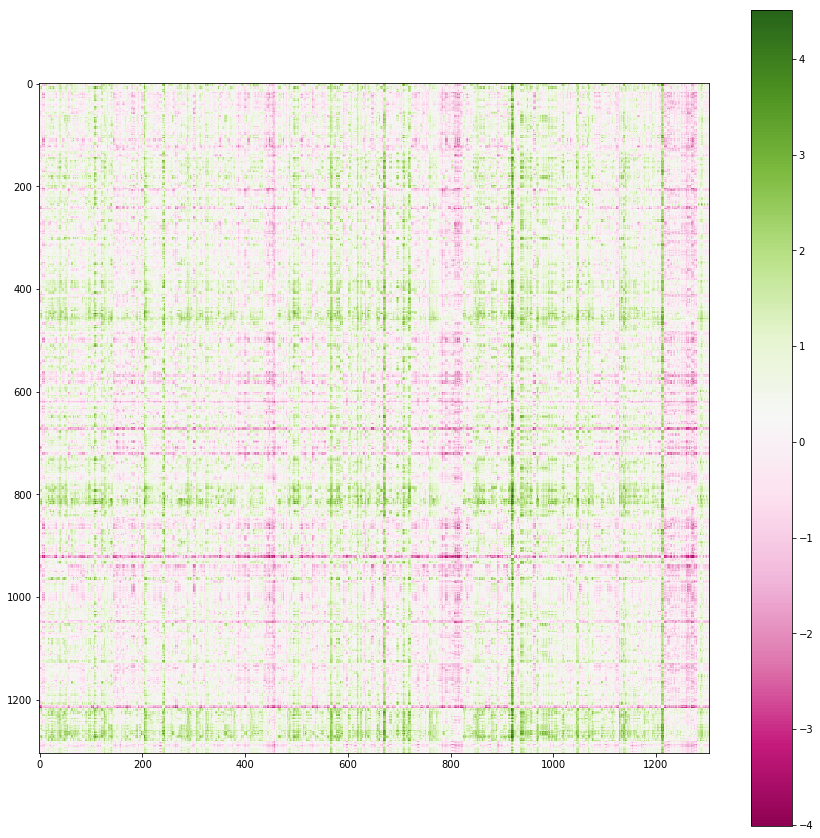
Depending on the calculation of the cells, the Nash equilibrium will change accordingly, and the result will have a different interpretation. In this post, I will experiment with two ways to calculate the cells. The first one uses Timeout as the win condition (the attacking player maximizes the damage per second (DPS), while the defending player maximizes the tankiness) and is best for gym battles, while the second one uses total damage output (TDO) and is best for boss raids.
- Metric 1: $ - \frac{\text{defender.def} \times \text{defender.sta}}{\text{attacker.atk} \times \text{attacker.dps}} $
- Metric 2: $ \log \left( \frac{\text{attacker.atk} \times \text{attacker.def} \times \text{attacker.sta} \times \text{attacker.dps}}{\text{defender.atk} \times \text{defender.def} \times \text{defender.dps}} \right) $
In the first scenario, I include legendary Pokémon for neither the gym defending side nor the attacking side. The reason for excluding legendaries from the attacking side is because they are not easily accessible. That said, nothing prevents the same computation and analysis from being applied to cases where legendaries are allowed.
In the second scenario, I consider all bosses possible and with equal tiers. This includes bosses that have rotated out and have yet to enter the game as well as bosses that may eventually change their tiers.
Results
Timeout for gym battles (DPS vs. tankiness)
The equilibrium attackers by the order of relevance: Blaziken, Breloom, Salamence.



The corresponding moves and their importance weights:
| Weight | Pokémon | Type1 | Type2 | Fast | Type | Charge | Type |
|---|---|---|---|---|---|---|---|
| 0.63 | Blaziken | Fire | Fighting | Counter | Fighting | Overheat | Fire |
| 0.25 | Breloom | Grass | Fighting | Counter | Fighting | Dynamic Punch | Fighting |
| 0.12 | Salamence | Dragon | Flying | Dragon Tail | Dragon | Draco Meteor | Dragon |
The equilibrium defenders by the order of relevance: Blissey (0.61), Dragonite (0.23), Gardevoir (0.16).



The moves of defenders are not relevant since the win condition is Timeout.
Total Damage Output for boss raids
The equilibrium attackers by the order of relevance: Kyogre, Mewtwo, Groudon, Rayquaza, Tyranitar.





The corresponding moves and their importance weights:
| Weight | Pokémon | Type1 | Type2 | Fast | Type | Charge | Type |
|---|---|---|---|---|---|---|---|
| 0.23 | Kyogre | Water | Waterfall | Water | Thunder | Electric | |
| 0.16 | Kyogre | Water | Waterfall | Water | Blizzard | Ice | |
| 0.03 | Kyogre | Water | Waterfall | Water | Hydro Pump | Water | |
| 0.20 | Mewtwo | Psychic | Psycho Cut | Psychic | Shadow Ball | Ghost | |
| 0.17 | Groudon | Ground | Dragon Tail | Dragon | Solar Beam | Grass | |
| 0.11 | Rayquaza | Dragon | Flying | Dragon Tail | Dragon | Outrage | Dragon |
| 0.10 | Tyranitar | Rock | Dark | Bite | Dark | Crunch | Dark |
Discussions
Timeout for gym battles (DPS vs. tankiness)
In this criterion, attackers only care about finishing the battle as quickly as possible. He does not consider the defending Pokémon as a threat because either they are not enough motivated or his attackers have much higher level.
Without legendaries, Blaziken, Breloom, and Salamence are the meta relevant attackers. They together have no bad matchup. Breloom is chosen instead of Machamp simply because it has slightly higher attack. If it faints, just use another Breloom. You can safely replace it with Machamp for better survivability. Indeed, you can consider Machamp as 1.x Breloom and as a better investment. The same reasoning goes with Salamence (instead of Dragonite).
The three attackers and the three defenders form a triangle like Rock-paper-scissors:
- The best defender is Blissey.
- To counter Blissey, use Breloom as the attacker.
- To counter Breloom, use Dragonite as the defender.
- To counter Dragonite, use Salamence as the attacker.
- To counter Salamence as well as Breloom, use Gardevoir as the defender.
- To counter Gardevoir as well as Blissey, use Blaziken (counter, overheat) as the attacker.
- To counter Blaziken, use Dragonite as the defender.

Of course, Blaziken is not optimal for Gardevoir. It is chosen firstly because its FIGHTING fast move deals super effective damage to Blissey, then because its FIRE charge move deals neutral damage to Gardevoir. This Blaziken is neither pure FIGHTING nor pure FIRE. That is, it trades some advantage against Blissey for less disadvantage against Gardevoir. Although not proved, I believe that any other Pokémon with both a FIGHTING move and a move not resisted by Gardevoir will do as well.
Pokémon not being on this list does not mean they are weaker. It just means, with these combinations, you have no bad matchup (by sacrificing some good matchup). This is the philosophy of minimalist lists.
Total Damage Output for boss raids
FIGHTING Pokémon are not chosen as an attacker; This is because the algorithm reckons that the hardest bosses are Mewtwo, Kyogre, Rayquaza, Raikou, Groudon, Ho-Oh, none of which is NORMAL type.
Although not intended, you can also use this list against Pokémon with high motivation in a regular gym battle. In face of a highly motivated defender, your high DPS team may have some survivability issue. In this case, just pretend the defender is a raid boss and use a high TDO attacker instead.
In this post, I used DPS for gym battles and TDO for boss raids. This is not an iron rule; you can well use TDO for gym battles and DPS for boss raids. You can also mix these two criteria into a hybrid one and thus get the best of both worlds.
Conclusion
This post used the Nash Equilibrium to build minimalist PvE lists, for both gym battles and boss raids. With these minimalist lists, you can concentrate your resource (i.e., Stardust) and have no bad matchup.
For gym battles, Blaziken, Breloom (or Machamp), and Salamence (or Dragonite) are the chosen attackers; Blissey, Dragonite, and Gardevoir are the chosen defenders.
For boss raids, a safe investment would be Kyogre, Mewtwo, Groudon, Rayquaza, Tyranitar.
These lists reflect only the criteria (e.g., DPS, TDO) chosen; with different criteria, the lists will also be different. Therefore, do not blindly follow these lists; use them as a guideline to build your own minimalist team.
Nash equilibrium is merely a tool, albeit an elegant one, to build minimalist lists; it is not the lists itself. Readers are encouraged to use this tool to build their own lists.
Resources
My code and dataset are hosted on GitHub. Feel free to contribute to it and use it for your own research.
Acknowledgment
- Thanks to Reddit user UW_Unknown_Warrior for contributing the dataset.
- Thanks to Vince Knight for helpful discussion.
- Thanks to Reddit user kairality, BruteBooger, Tangent444, Edocsil47, LanAkou, passwordisaardvark, and shrakner for useful feedback.
- Thanks to martinsweitzer for pointing out dependency issues.
FAQs
Q: Are the Pokémon on the attacker list optimal counters?
A: No. They are by no means the optimal counters. Instead, they are the worst case optimal in that their toughest gym defender is relatively the easiest.
Q: What do the weights mean?
A: They are the importance and usefulness of these Pokémon. You should prioritize the investment on Pokémon with high weights. It is also recommended to get multiple copies of Pokémon with high weights.
Q: What is this list different from other tier lists?
A: Rigorously speaking, this is not a tier list. Tier lists are progressive, including both the optimal choices and the suboptimal choices, whereas this tier list is a meta relevant list. If you are using Pokémon absent on this list, you are either using suboptimal Pokémon or you are taking advantage of the information of the opponent’s team composition (which is not always available).
Q: What if I cannot obtain Pokémon on the meta relevant list?
A: Do not take the lists given in the post too serious. They are meant to showcase how the Nash equilibrium can be used; You are encouraged to build your own meta relevant list: by defining your goal and removing the Pokémon inaccessible and rerunning the same computation, you can obtain the meta relevant list tailored for you! In this way, you can build a personal optimal team.
Q: Why are the legacy moves not included?
A: Without considering the legacy moves, there are already 1000+ Pokemon (with different combinations of movesets). To consider certain Legacy moves, you can reuse my code by adding Pokémon with legacy moves into the dataset.
Q: The Pokémon proposed all have single-bar charge moves, which are not very desirable in gym battles because they may result in overkills.
A: To avoid single-bar charge moves, just include only Pokémon with multi-bar charge moves in your attacker pool and rerun the computation.
Q: There are 6 slots for gyms, whereas there are only 3 Pokémon on the defender list. I can’t put a second Blissey in!
A: Use Snorlax as a substitute for Blissey.
Q: My Blaziken died from Gardevoir!!!
A: This is because either your Blaziken’s level is not high enough or the Gardevoir is highly motivated. Try to dodge Gardevoir’s charge move or use a Pokémon with high TDO in the 2nd list against this Gardevoir.
Q: Could this list be used in PvP?
A: Currently we do not have enough information about the PvP. Nevertheless, the Nash Equilibrium concept originates from PvP and is thus promising for that incoming game mechanism.