Many newcomers of the Julia language feel confused about the value type described in the official documentation. They don’t understand what it is used for and why other languages don’t have this feature. In fact, as a “secret” rarely shared by the core developers, you may probably never need the value type.

In this post, to help the readers understand what the value type does and why it is mostly unnecessary, I will use it to mimic two anti-patterns (i.e., which are considered bad practice) in object-oriented programming (OOP). These two anti-patterns are infinite dispatch paths and God object.

Contents

• Infinite dispatch path
• God object
• Conclusion

Infinite dispatch path

Let’s implement a root function with only one argument. I will first show an object-oriented design via C++. Then I will give a Julia equivalent making use of the value type.

As we all know, a root function $x^{1/n}$ takes two arguments: the base $x$ and the degree $n$. Let’s suppose that $n$ is a positive integer. Traditionally, we can implement it as follows:

double root(double x, int n);

It takes the two arguments and return a real number. Internally, it may employ, say, Newton’s method and finds the answer efficiently.

Now I add one requirement: the function must be univariate and be similar to

double root(double x);

As an expert of OOP, you may come up with the following idea:

class IRoot{
  public:
    virtual double root(double x) = 0;
};

class SquareRoot : IRoot{
  public:
    double root(double x);
};

class CubeRoot : IRoot{
  public:
    double root(double x);
};

// ...more subclasses

You set an interface IRoot and use various subclasses to implement the various root functions (e.g. square root, cube root).

This design works, except that you need to define an infinite number of subclasses (one for each natural number), which is impossible. Even if it’s possible, when the function is called via a pointer or a reference to IRoot, the program will have to look through an infinitely long table to find the matched method. In other words, we created an infinite dispatch path, which is a bad design.

Before introducing the Julia equivalent, I must admit that this root is not truly univariate. Experienced programmers know that this root takes implicitly an additional this pointer as parameter. The actual function signature is, instead,

double root(IRoot *this, double x);

C++, as well as many other languages, single dispatches on the this parameter. Indeed, by recognizing, during the runtime, the actual class this points to, the program can dispatch the caller to the correct callee.

An equivalent Julia implementation can be as simple as follows:

root(x::Real, ::Val{n}) where n

where we define a value type Val{n} with n being the degree. Inside the function, we can extract the degree as n and use it for computation. For example, a cheater’s version can be written as follows:

root(x::Real, ::Val{n}) where {n} = x^inv(n)

To call the function, we can write, say, root(3.0, Val(2)), which stands for the square root of $3.0$.

Unlike the original version (i.e. passing n directly to the function), which will be compiled into one machine code for all n, the Julia version will compile one machine code for each n. During the runtime, the program identifies the value of n, generates the machine code for its specific value, and dispatches to this machine code.

Although slightly better than the C++ version, it still generates infinite dispatch paths. You might don’t want to write this kind of code without a good reason.

God object

Another anti-pattern in OOP is the so-called God object. In this section, I will use Julia’s value type to create something similar.

A God object is an object that knows all and encompasses all, as explained in the book Design Pattern Explained Simply. The Main Controller Class in the figure below has all needed fields (e.g. Status, Mode), can do all things by itself (notice the various zero-parameter functions), and is thus a God object.

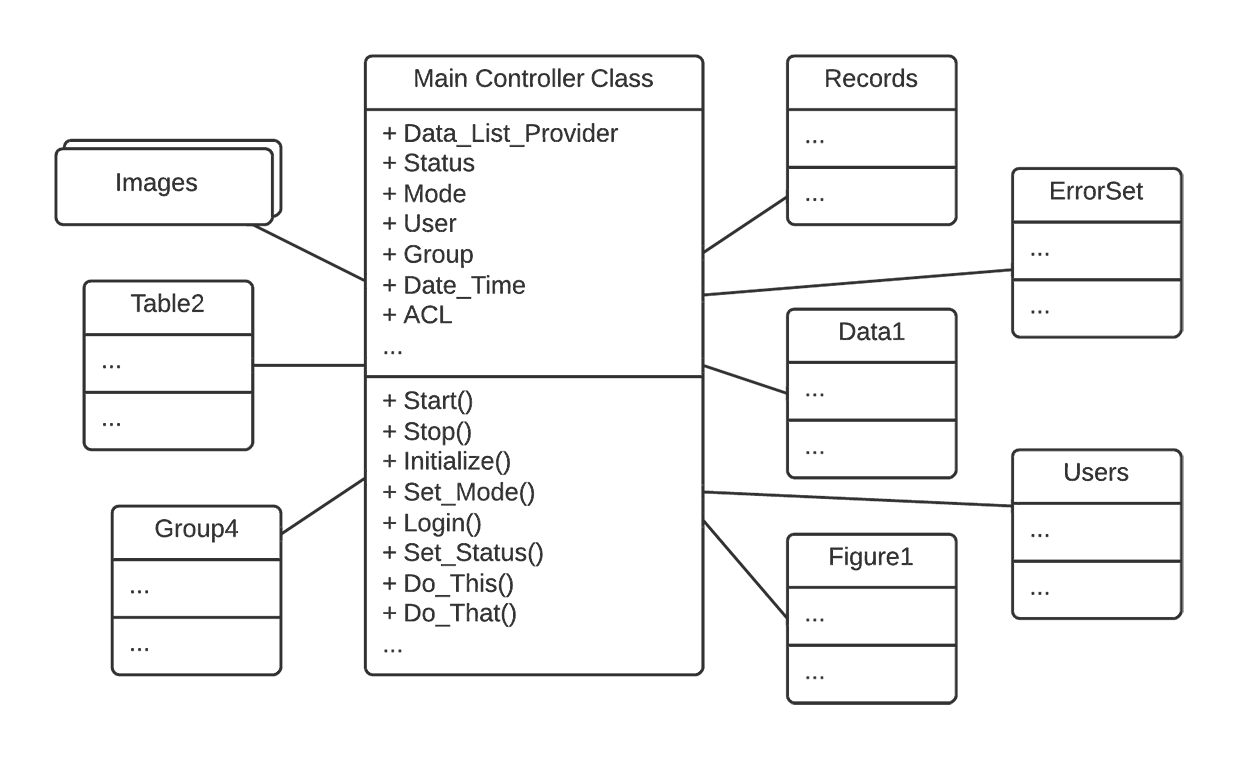
In Julia, there is a dual concept to the God object – the one true function. If the God object can do all things, then the one true function can work on all objects. It can be defined as follows either with or without the value type:

the_one_true_function(::T) where T
the_one_true_function_2(::Val{N}) where N

where T can be any type and N can be any “plain bits” values (types, symbols, integers, floating-point numbers, tuples, etc.). These functions expect any type or any value and thereby announce to the world that they can do anything.

Notice that how it is different from the following definition:

an_ordinary_function(::Any)

which uses duck typing. The function an_ordinary_function admits the possibility of failure when the argument does not follow the protocol, whereas the_one_true_function explicitly declares that it works for all types.

By the way, the opposite to the one true function is the so-called overspecialization, which is also bad practice. For example, we can define the root function as

root(x::Float64, n::Int)

where I used the Float64 type instead of the more general abstract type Real. This causes overspecialization, which excludes any possibility for it to work on other real numbers (e.g. Float32, BigFloat, Integer, Rational, Irrational).

Conclusion

The value type has few use cases and is generally used by core developers. As a general developer or a data scientist, you may never need this feature.