Simpson's Paradox and Impostor Syndrome
As a chronic sufferer of impostor syndrome, I always know what it is and how it is formed. Nevertheless, I never get ashamed; actually, it pushes me forward and helps me surpass myself again and again. To some extent, I am grateful and even feel proud of it. Although I am a master of impostor syndrome and proactively use it as a weapon, I never found a proper mathematical model to describe it until I came across Simpson’s paradox once again recently. In this post, I will explain both concepts and make the link between them.
Impostor syndrome
Impostor syndrome is a psychological pattern in which an individual doubts his skills, talents, or accomplishments and has a persistent internalized fear of being exposed as a “fraud”. There are two key elements in this definition. One is high skills, high talents, high accomplishments, and the other is self-doubt.
Impostor syndrome can affect both men and women, while it is more prevalent among high-achieving women according to traditional research. Without loss of generality, in this post, I will focus on the demographic subgroup of high-achieving women. One can safely replace it with any other subgroup as long as it satisfies the corresponding conditions which will be clear by the end of the post.
Simpson paradox
Simpson’s paradox is a phenomenon where a property appears in several groups when analyzed alone but disappears or reverses when the groups are combined. There can be many forms of Simpson’s paradox, with the most famous probably being the UC Berkeley gender bias.
In the fall of 1973, the University of California, Berkeley had 12763 applicants and an admission rate of 41%. Gender analysis showed that the male applicants were more likely to enroll than the female applicants, with the male admission rate being 44% and the female 35%. This difference was so large that it could not be explained by chance.
| Subgroup | Applicants | Admitted |
|---|---|---|
| Total | 12763 | 41% |
| Men | 8442 | 44% |
| Women | 4321 | 35% |
It is attempting to draw the conclusion that men are better than women overall.
However, the following table showing the six largest departments tells a different tale.
The admission rates of Department B–E are not that different, while Department A has a significant favor for women.
These statistics tend to convince us that women are better than men overall.
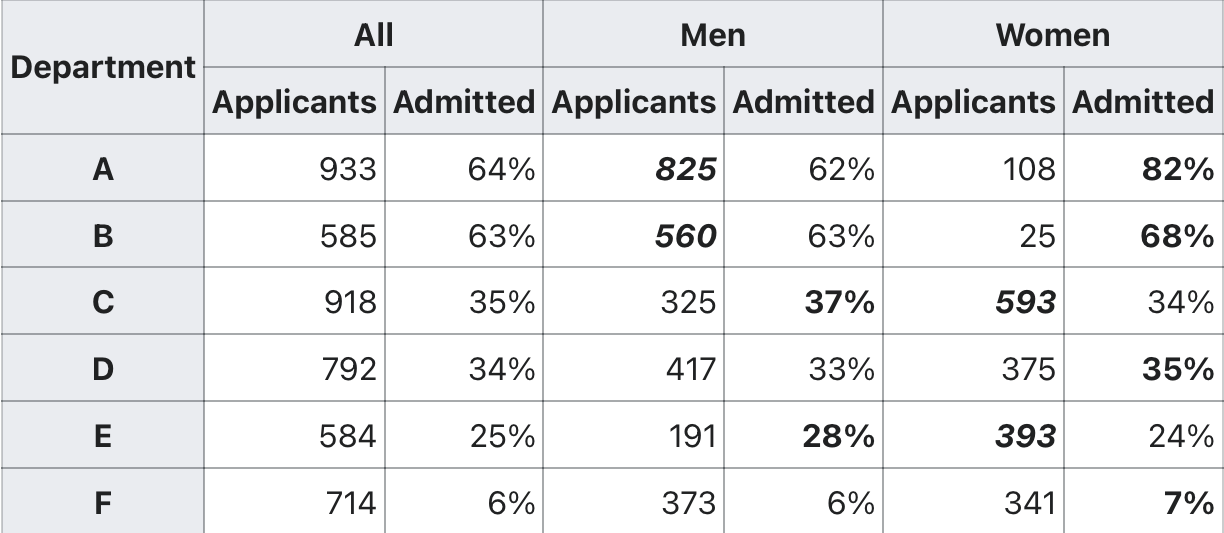
We get different conclusions depending on whether we use the combined or segmented data, hence the Simpson’s paradox.
Mathematical explanation for Simpson’s paradox
The above paradox actually results from the fact that women tended to apply to more competitive departments with low rates of admission. Thus, their overall rate of admission is dragged downwards.
Let us illustrate it in a 2-dimensional vector space. A success rate of $\frac{p}{q}$ (i.e., success/attempts) can be represented by the slope of the vector $\vec{A} = (q, p)$. A steeper vector then represents a greater success rate. If two rates $\frac{p_1}{q_1}$ and $\frac{p_2}{q_2}$ are combined, the resulting rate will be $\frac{p_1 + p_2}{q_1 + q_2}$ and the resulting vector will be $(q_1 + q_2, p_1 + p_2)$.
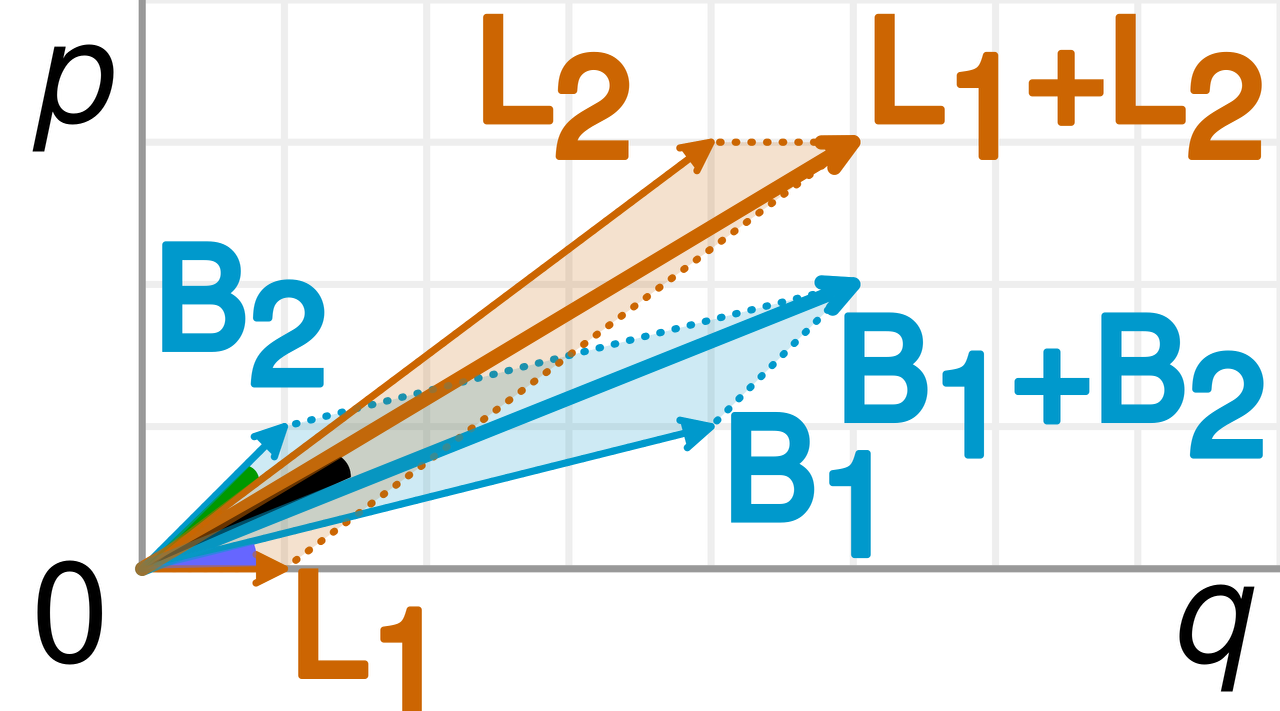 In the above figure, both $B_1$ and $B_2$ are steeper than $L_1$ and $L_2$, respectively.
However, their sums, $B_1 + B_2$ is less steeper than $L_1 + L_2$.
In the above figure, both $B_1$ and $B_2$ are steeper than $L_1$ and $L_2$, respectively.
However, their sums, $B_1 + B_2$ is less steeper than $L_1 + L_2$.
This illustration accurately explained why women’s overall admission rate can be lower than men’s even if their admission rate of each individual department is higher than men’s.
Link between impostor syndrome and Simpson’s paradox
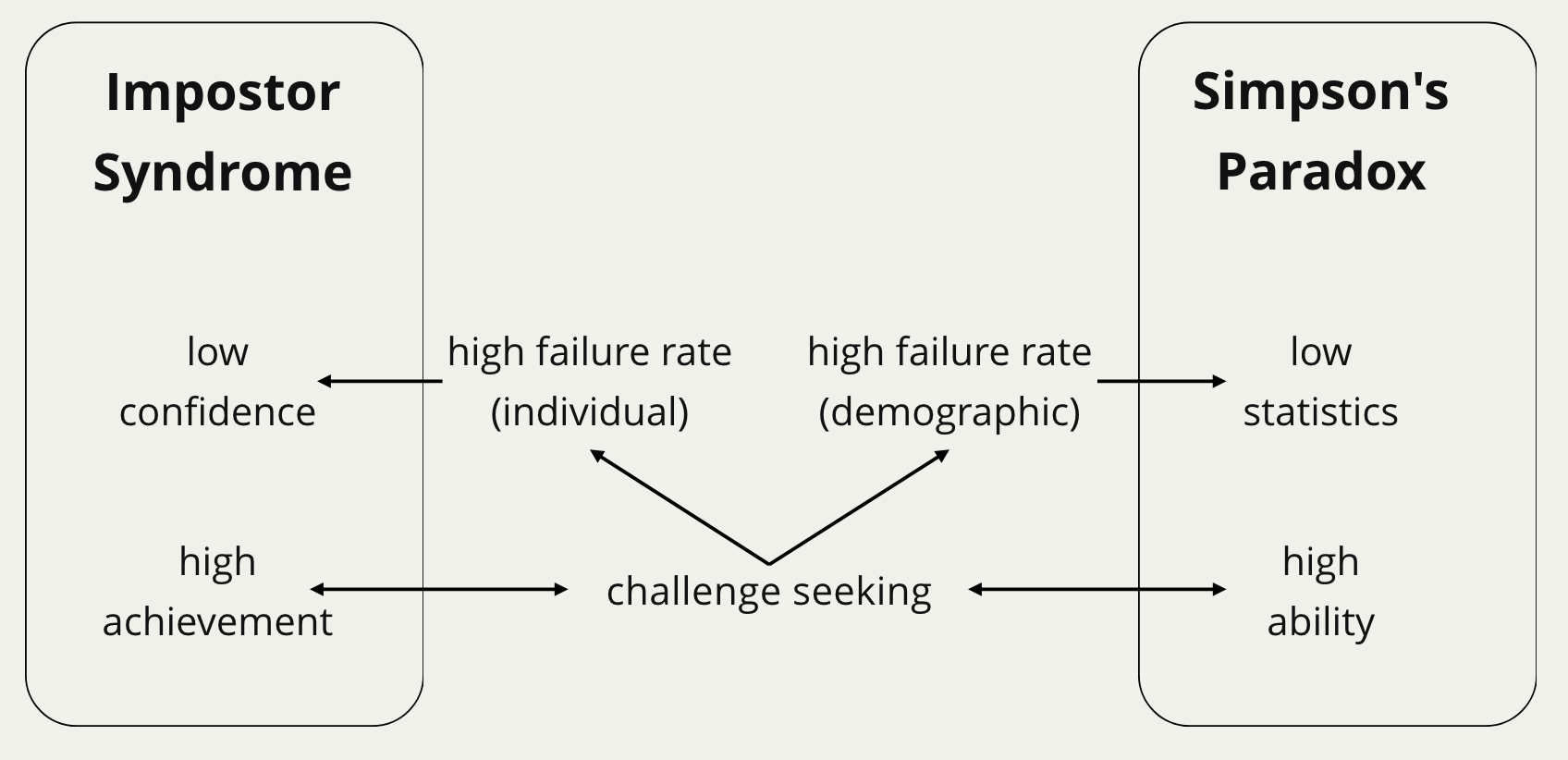
There are two key elements in Simpson’s paradox, with one being high ability and the other low overall statistics. Here, we observe a surprising similarity between impostor syndrome and Simpson’s paradox.
| Paradox | High | Low | Sufferer |
|---|---|---|---|
| Impostor | achievement | confidence | women |
| Simpson | ability | statistics | women |
As we just saw in the UCB example that Simpson’s paradox results from the fact of women being challenge-seeking, we can also say that impostor syndrome results from this very challenge-seeking nature.
Women seek challenges, which result in high failure rates, which in turn become an emotional burden on themselves, which is eventually diagnosed as impostor syndrome.
Simpson’s paradox and impostor syndrome reflect the two uses of the law of large numbers. Simpson’s paradox uses it on the cohort data and calculates the failure rate across all individuals, while impostor syndrome uses it on the temporal data and calculates the failure rate for one individual in an ergodic sense.
The high failure rates resulted from the challenges lead to low statistics in Simpson’s paradox and low confidence in impostor syndrome. Although the statistics and the confidence plummet, this challenge-seeking nature nonetheless is both the cause and effect of the high-achievement and high-ability aspects.
Previously, I assumed the victims to be women. Here, having known the true cause, we can safely replace women with the subgroup of challenge-seeking persons, which can be both men and women.
Impostor syndrome as an instance of Simpson’s paradox
In this post, I exclusively used the UC Berkeley example. In fact, Simpson’s paradox has many other forms. Impostor syndrome is actually a special case of Simpson’s paradox, which is therein applied on a single individual’s temporal data.
With this understanding, one can probably mitigate the effect of impostor syndrome by breaking the time series down and making cross-sectional comparison with other people on each individual task, or in plain words, by reminding oneself of his past achievements.
Summary
In this post, I first explained the concept of Simpson’s paradox and impostor syndrome. Then, I pointed out the similarity between these two: they both result from the challenge-seeking nature. This nature results in high failure rates, individually or demographically, which are the direct cause of impostor syndrome and Simpson’s paradox, respectively. Finally, we can regard impostor syndrome as a special case of Simpson’s paradox, since it has many manifestations other than the UCB example.