A walk-through of Hao Huang's solution to the sensitivity conjecture

Earlier this month (July, 2019), mathematician Hao Huang posted a proof of the Sensitivity Conjecture, which has troubled mathematicians for 30 years. To people’s surprise, this proof is only 2 page’s long and involves only undergraduate level math. On the Internet, you can find some reports, written for the general public, about the background story and the interpretation of the sensitivity conjecture. Also, several experts, such as Terence Tao, are elaborating on it. Here, writing for students and non-experts, I will summarize the key steps in Hao Huang’s proof, in an attempt to help them quickly grasp the essential.

Boolean function

A Boolean function $f: \{0,1 \}^n \rightarrow \{0,1 \}$ is a function whose input and output are both binaries. For example, the following image from Quanta Magazine is an excellent illustration of a Boolean function.

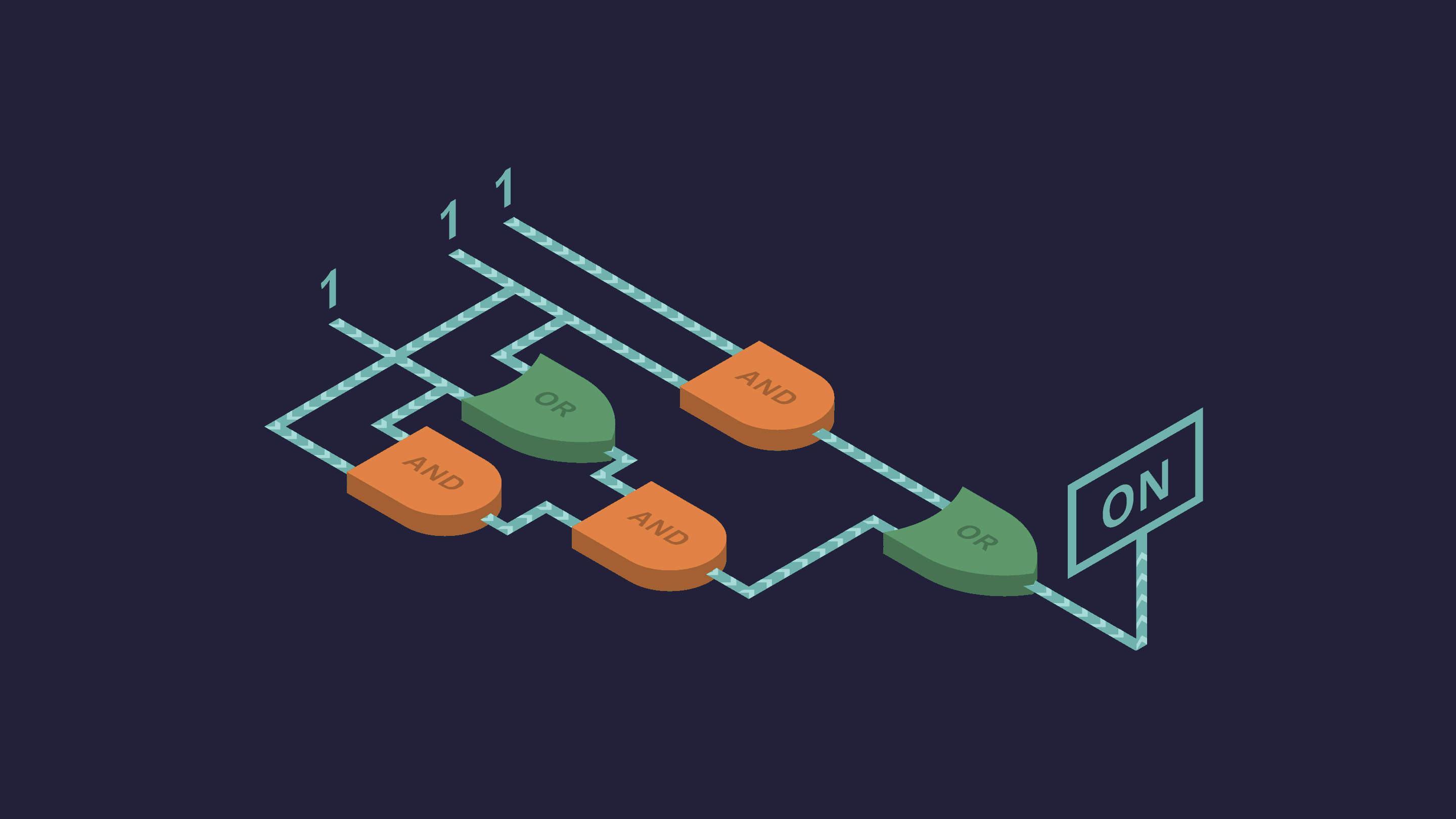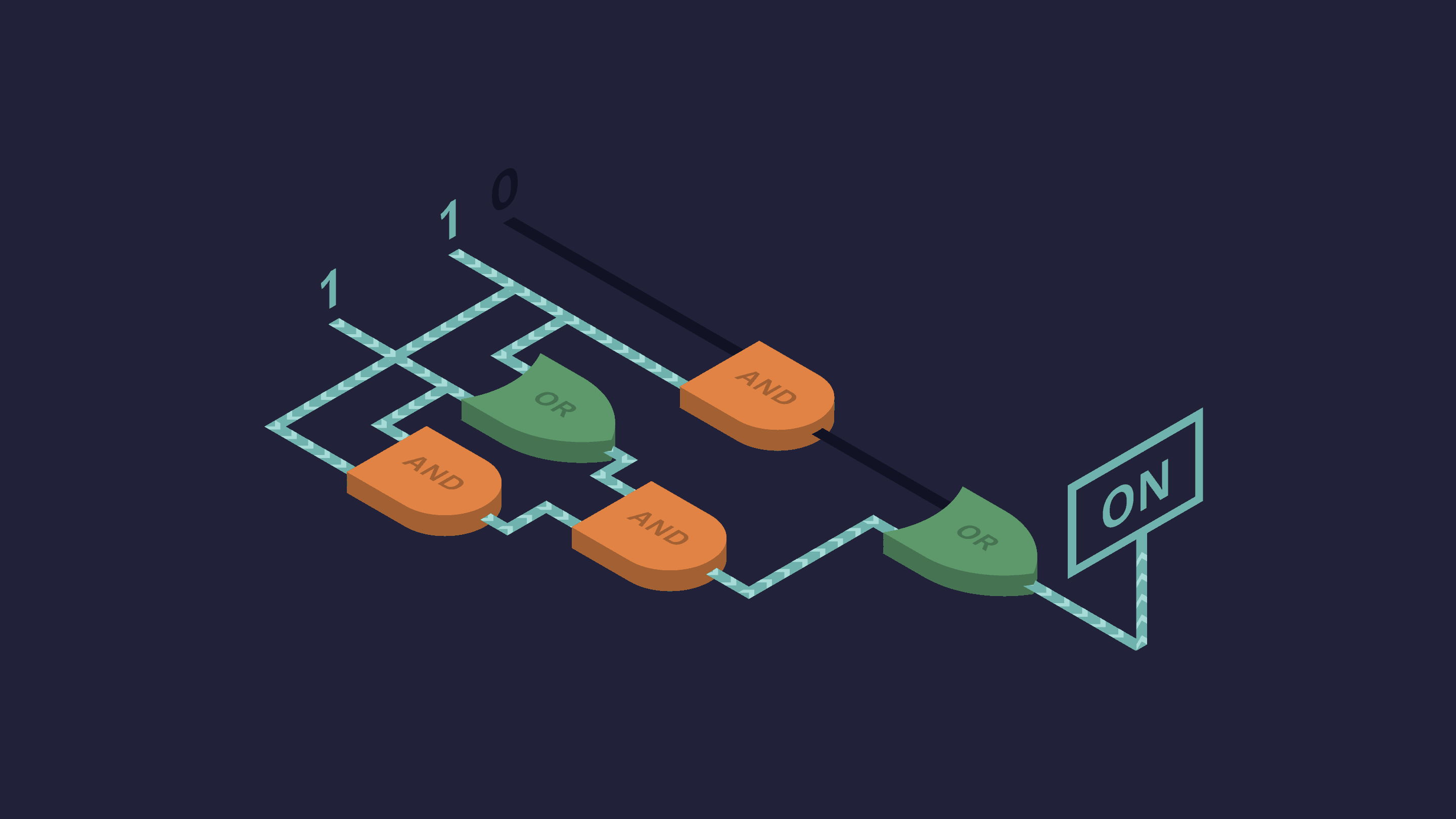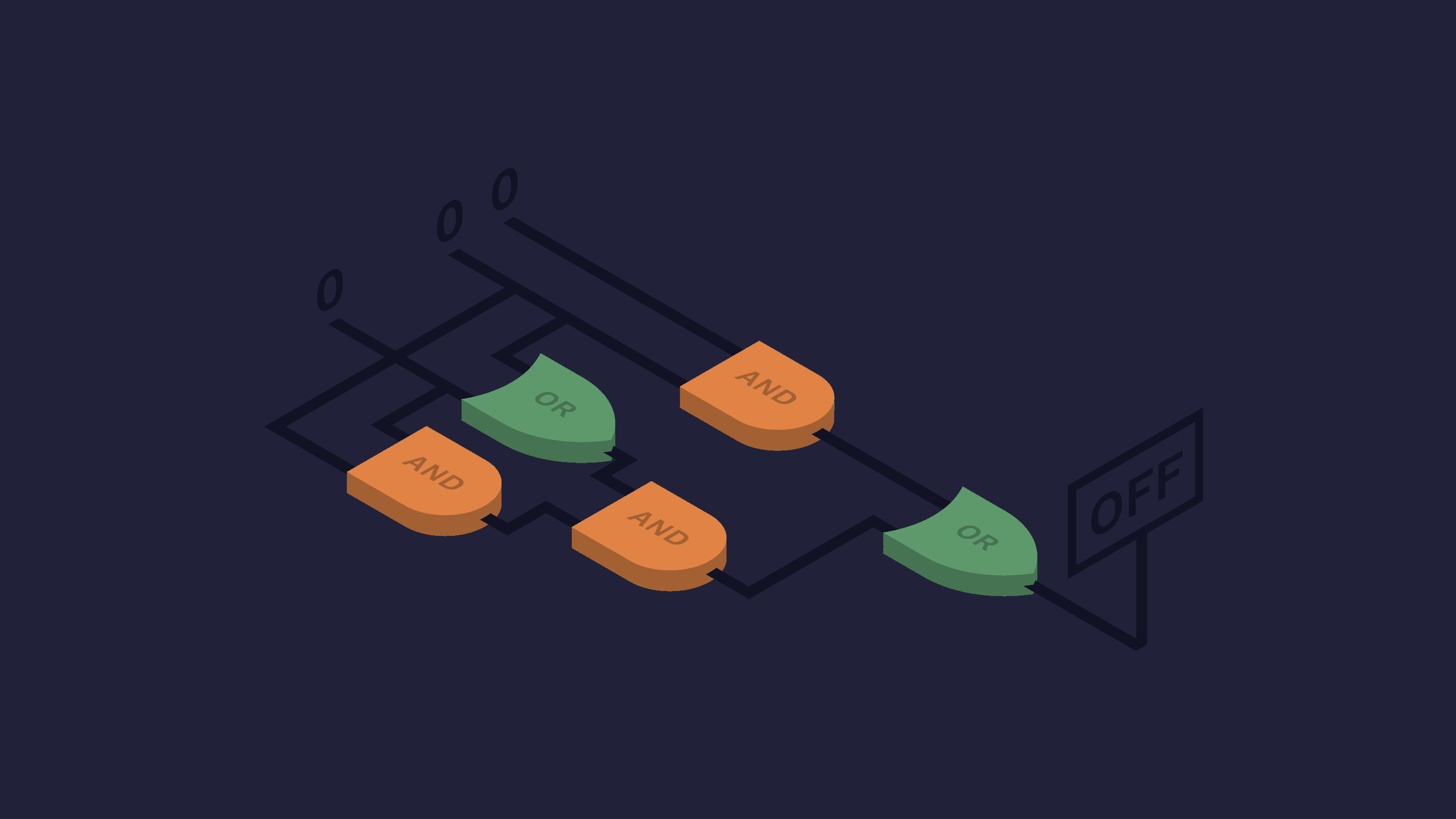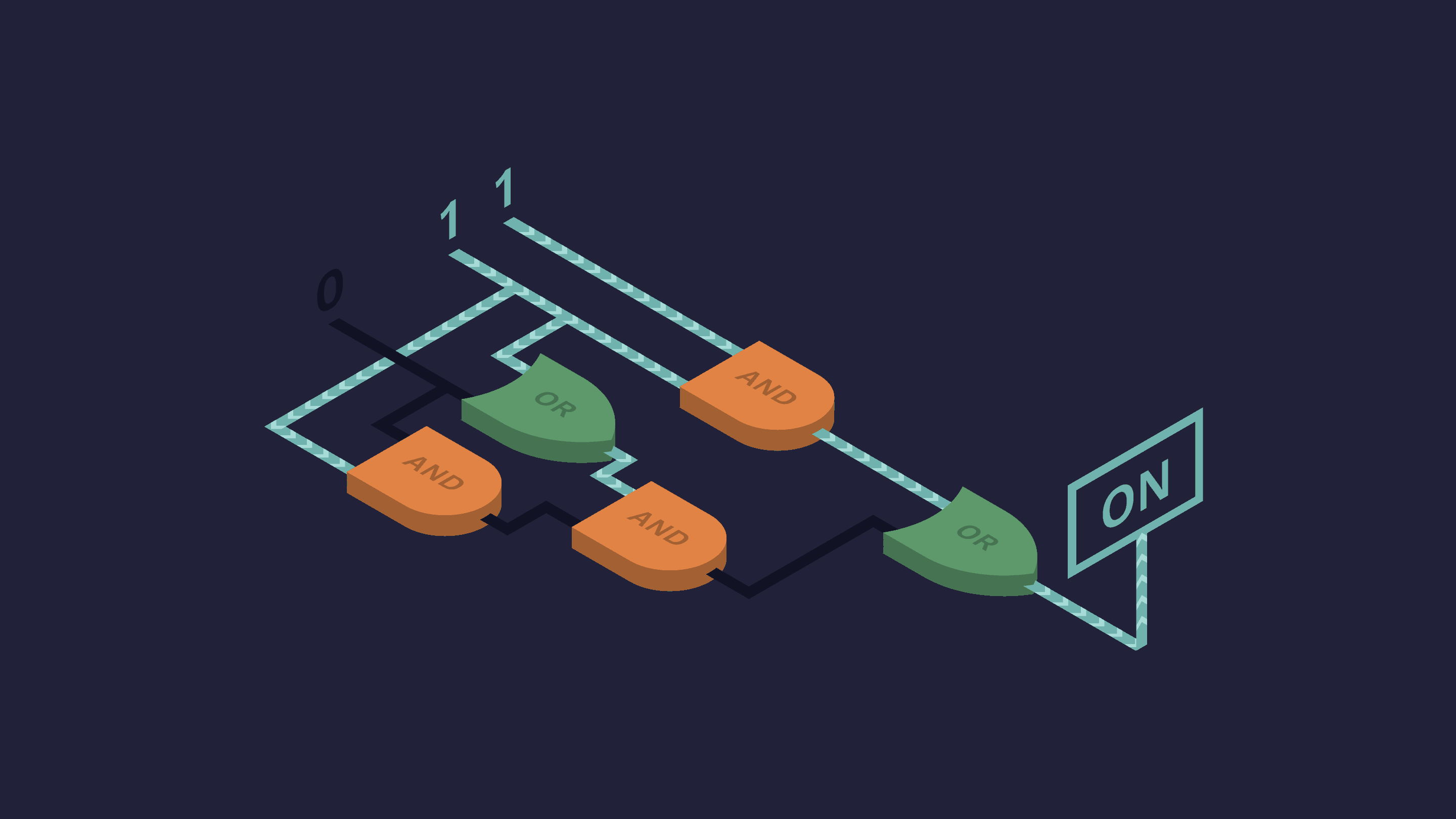
From a more mathematical point of view, a Boolean function is a binary colorization of the $n$-dimensional hypercube.

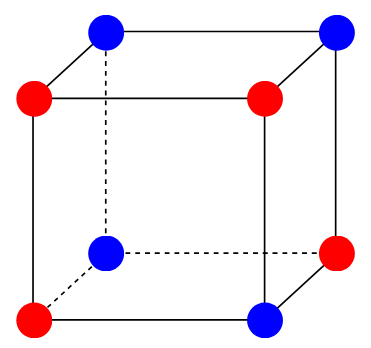
Sensitivity of Boolean functions

Before explaining the sensitivity, let us first explain the local sensitivity. The local sensitivity is like the derivative. For example, in the figure above, the red bottom-left vertex has a local sensitivity of 2 because two of its neighbors have a different color. The blue bottom-right vertex has a local sensitivity of 3.

The (global) sensitivity is like the Lipschitz constant. It is the maximum of all local sensitivities. The above figure has a sensitivity of 3.

Sensitivity conjecture

To describe a person, we can use adjectives such as cute, honest, smart, etc. To describe a Boolean function, we can similarly use metrics such as sensitivity, degree, etc.

People often wonder whether the various qualities of a person are related. For instance, one of the most popular is whether beautiful persons are also kind. Similarly, mathematicians wonder whether the various metrics of the Boolean function are related.

By relation, I meant a polynomial relation. That is, in the term of popular culture, whether [ \text{beauty} \le \text{kindness}^a, \quad \text{kindness} \le \text{beauty}^b ] for some constants $a$ and $b$. If the relation is not polynomial but exponential, maybe the relation is too weak and not even remotely relevant. By replacing the words such as beauty and kindness with metrics for the Boolean function such as sensitivity and degree, you discover mathematician’s fetish.

It is long known that all metrics but the sensitivity are mutually polynomially related and form a family. The sensitivity conjecture states that the last rebel sensitivity is also a member of this family.

What we already knew

We already knew that the sensitivity can be upper-bounded by (a polynomial of) the other metrics. That is, if the other metrics are not too large, the sensitivity cannot be too large either. [ \text{sensitivity} \le \text{polynomial}(\text{some metric}) ]

What remained unknown was whether the sensitivity could be used to upper-bound the other metrics or, equivalently, whether the sensitivity could be lower-bounded by the other metrics. That is, if the sensitivity is not too large, whether the other metrics are also not too large. [ \text{polynomial}(\text{some metric}) \le \text{sensitivity} ]

Mathematicians have thought about it for so long that they even discovered an equivalent problem [Gotsman and Linial 1992]: For any subgraph of the $n$-dimensional hypercube with (strictly) more than half vertices, whether its largest degree is at least $h(n)$, with $h$ being a polynomial.

What Hao Huang proved

Yes. [ h(\cdot) = \sqrt{\cdot} ] This result is tight.

How Hao Huang proved it

To prove [ \text{degree}(\text{a subgraph with more than half vertices}) \ge \sqrt{n}, ] Hao Huang introduced some middle men: not one, but two!

The 1st middle man comes. The 1st middle man is the top eigenvalue of the associated adjacency matrix – let us call it $H$ – of the subgraph. It is a classical result that the 1st middle man is smaller than the degree of the subgraph.

The 2nd middle man talks to the 1st middle man. The adjacency matrix has coefficients of either 0 or 1. If we flip the signs of some 1’s, we get another matrix $A$, whose top eigenvalue, defined as the 2nd middle man, is smaller than the one of the original adjacency matrix (i.e., the 1st middle man).

The 2nd middle man talks to $\sqrt{n}$. The 2nd middle man is an impostor, who would do whatever it takes to be as close to $\sqrt{n}$ as possible. Indeed, he flips its moral standards (i.e., the sign of 1’s of $H$) in such a way that he can be exactly $\sqrt{n}$. More concretely, the carefully flipped matrix $A$ is a submatrix of a so-called pseudo-adjacency matrix $A_n$ that has half eigenvalues equal to $\sqrt{n}$ and the other half equal to $-\sqrt{n}$. By Cauchy’s Interlace Theorem, $A$ is sure to have at least one eigenvalue equal to $\sqrt{n}$.

Thus, Hao Huang successfully proved the sensitivity conjecture.

Let us praise the 2nd middle man

Above, I teasingly called the 2nd middle man an impostor, which has a very bad connotation. Here, I want to emphasize that he is a benevolent impostor. He did not flip his moral standards to get maximal personal gain. Instead, he did it for the purpose of easing the communication of his clients. Without him, Cauchy’s Interlace Theorem would have been useless here.

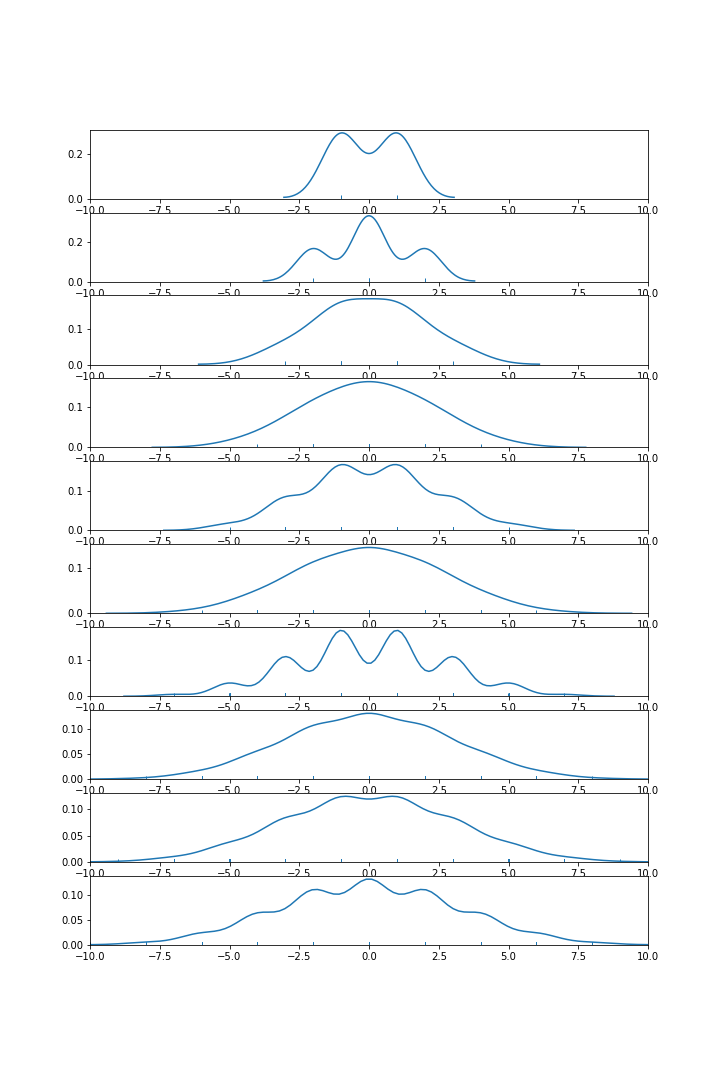
To see this, below I plotted the distribution of the eigenvalues of the original adjacency matrix (before the flip) of the $n$-dimensional hypercubes, for $n=1, 2, \ldots, 10$. We can observe that the $2^{n-1}$-th largest eigenvalue barely increases with $n$. In other words, we are unlikely to get a polynomial relation without the flip.

Wenjie Zheng