How to organize faction PvP events in 1-on-1 oriented games
 Image from Gustavo Santos at DeviantArt
Image from Gustavo Santos at DeviantArt
This post aims to analyze Yugioh Duel Links’ Duel Carnival events. To analyze it at a higher level, I will abstract it as (what I call) faction PvP in 1-on-1 oriented games, in which players are divided into two factions to compete with each other but still on a 1-on-1 basis. I will show you that, for fair competition, intra-faction duels should be forbidden. Otherwise, provided that the population ratio is above the golden ratio (approximately 1.618), the more populous faction will always win the war regardless of the individual duel outcomes and the win/loss reward allocation. This conclusion applies not only to Duel Links but also to any other online PvP games such as Shadowverse, Hearthstone, Pokémon GO and so on.
Introduction
By the term faction, I mean a group of players with common interests but loosely organized. Contrary to teams, whose members have strong interaction among them and can perform complex strategies, there is little or no communication in factions. By the term Faction PvP, I mean a war in which players pick 1-on-1 duels for the benefit of their factions. This definition is different from the one in Minecraft and other MMORPGs, which focuses on the mixed battle between two groups of players.
Let us consider a PvP event with two factions: Faction A has $p$ players, and Faction B has $q$ players. The players duel with each other: the winner of each duel gets $a$ points, and the loser receives $b$ points with $b \le a$. The faction getting the highest aggregated points at the end of the event wins the war. You are the matchmaker, who decides which player will duel against which player. Will you just pick two immediately available players (potentially from the same faction) and start the duel as soon as possible (Rule I), or will you wait until two players from different factions are available (Rule II)?
In the remaining of the post, I first argue that, for fair competition, intra-faction duels should be forbidden, and then I give several measures to control the potentially increased waiting time.
Should intra-faction duels be allowed?
To answer this question, let us first solve the following mathematical problem. Given the ratio of the final aggregated points of both factions $v \in [0, +\infty]$, estimate the ratio of the populations of both factions $r:=\frac{p}{q} \in [0, +\infty]$, assuming that
- Rule I is used for matching;
- Faction A players are uniformly stronger than Faction B players, namely each inter-faction duel finishes with A’s win.
If we can solve the problem, then, by setting $v=1$ (i.e., draw), we can get the population threshold for Faction A to lose the war. You may wonder how A can lose the war since A wins every single duel against B. The intuition behind is that a lot of points can be generated simply by B’s intra-faction duels, where both the winning points and the losing points go to Faction B. Of course, Faction A can do the same, but its chance to get intra-faction duels is lower than B if A has a smaller population than B. Therefore, the faction with a larger population has an undeniable advantage under Rule I and sometimes can even completely ignore the outcomes of inter-faction duels.
| Faction A | Faction B | Ratio | |
|---|---|---|---|
| Population | $p$ | $q$ | $r:=\frac{p}{q}$ |
| Win | Loss | Ratio | |
| Points | $a$ | $b$ | $c:=\frac{a}{b}$ |
Now let us proceed to solve the mathematical problem above. By intra-faction dueling, Faction A gets $p^2(a+b)$ points, and Faction B receives $q^2(a+b)$ points; by inter-faction duels, Faction A gets $pqa$ points, and Faction B receives $pqb$ points. Therefore, we get the equation about the ratio of the final aggregated points: [ \frac{p^2(a+b)+pqa}{q^2(a+b)+pqb} = v. ] By dividing $q^2b$ within the fraction, we get [ \frac{r^2(c+1)+rc}{c+1+r} = v. ] Solving this equation, we get [ r = \frac{v-c+\sqrt{(v-c)^2+4v(c+1)^2}}{2(c+1)}. ] We solved the problem posed at the beginning of this section: given the outcome $v$ of the event, we can estimate the population ratio of both factions.
The following table gives the value of $r$ for various $c$’s when $v \equiv 1$.
| c | 1 | 1.5 | 2 | 2.5 | 3 | 3.5 | 4 | 4.5 | 5 |
|---|---|---|---|---|---|---|---|---|---|
| r | 1.00 | 0.90 | 0.85 | 0.81 | 0.78 | 0.76 | 0.74 | 0.73 | 0.72 |
When $c=1$ (i.e., there are equal reward points for the winner and the loser), Faction A must have more players to win the war, which is obvious. When $c$ increases, which favors Faction A, Faction A must have a higher population than the correspondent $r$ to win the war. For example, when $c=3$ (e.g., the winner gets 3000 points, and the loser receives 1000 points), Faction A’s population must be larger than 0.78 times of Faction B’s population to win the war. Moreover, when $c = +\infty$ (i.e., the loser does not get any reward), we get $r = \frac{\sqrt{5}-1}{2} \approx 0.618$, a number related to the golden ratio. In other words, if Faction A’s population is below 0.618 times of Faction B’s population, Rule I will give Faction B free win, and vice versa.
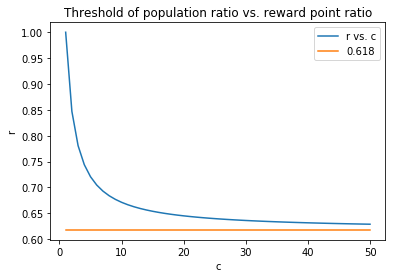
In conclusion, intra-faction duels give the more populous faction an undeniable advantage. In particular, when one faction’s population is greater than 1.618 times of the other faction’s population, the more populous faction wins the war regardless of the indiviual duel outcomes and the win/loss reward allocation. Therefore, intra-faction duels should be forbidden, and Rule II should be applied instead.
Measures to control the waiting time
Since intra-faction duels are now forbidden, you will have fewer players to duel with, and it is understandable that the duel matching time will increase. In fact, the mechanism will be completely different and should be treated with care.
Indeed, the waiting time is composed of two parts: the data collection time and the queuing time. The former is the time for the server to register your dueling request, and the latter is the time for one player, say, Alice, to wait for a second player, say, Bob. The data collection time for both players is fixed and will not change regardless of the matching rule. The queuing time for Alice depends on Bob, and the queuing time for Bob is 0 (he does not wait for anyone). Therefore, when Rule II is applied, only the queuing time is increased since Alice and Bob may be within the same faction, in which case Alice should wait for another player, say, Cathy.
What we perceive so far in DuelLinks is the data collection time, and the queuing time is negligible given the enormous player base. However, this queuing time can become phenomenal when Rule II is imposed. Let us consider two queues, one for Faction A and the other for Faction B. If one faction, say A, has larger population than the other, say B, the queue of A will keep growing and even overflows, and the queue of B is always empty; A is always waiting for B and will have terrible game experience. The cause of this phenomenon is that one of the factions has more than 50% of the total players.
The solutions to this problem are hence straightforward:
- setting 3+ initial factions (e.g., Pokémon GO) so that none is likely to have more than 50% of players;
- breaking large factions (e.g., >50%) into subfactions to maintian the balance;
- setting an upper bound to the queuing time (if the queuing time exceeds the bound, just let the player in question duel another player from the same faction, but the reward points gained are not added into that faction’s account).
I believe that these measures can solve the problem and give the players good game experience.
Conclusion
In faction PvP, intra-faction duels should be forbidden, and measures can be taken to control the queuing time.